Autor: Daniel Trujillo Zamorano.
RESUMEN
Una parte de las Ciencias de la Computación, específicamente la graficación por computadora, toma como base el conocimiento del álgebra lineal en el uso de las matrices para representar sistemas de ecuaciones lineales, en nuestro caso serán de utilidad como medio de almacenamiento y para el uso de las transformaciones lineales (operaciones con matrices) que dan lugar al escalamiento, traslación y rotación de figuras geométricas o imágenes.
PALABRAS CLAVE: Algebra lineal, graficación por computadora, transformaciones lineales, traslación, escalamiento, rotación.
INTRODUCCIÓN
La Informática como una ciencia en pleno desarrollo toma como base el uso de matrices para almacenar y operar datos, en este caso, vértices de una figura geométrica a través de algoritmos computacionales. El objetivo principal de este trabajo es demostrar claramente que el álgebra lineal se aplica para almacenar y realizar transformaciones en los gráficos como son la traslación, el escalamiento y la rotación a través de ejemplos donde se demuestre y explique de manera comprensible la influencia del álgebra lineal en las gráficas por computadora y específicamente en un sinnúmero de programas computacionales que requieren el uso de gráficos.
DESARROLLO
Transformaciones lineales
Sean V y W espacios vectoriales reales. Una transformación lineal T de V en W es una función que asigna a cada vector v ϵ V un vector único Tv ϵ W y que satisface, para cada u y v en V y cada escalar α.
Almacenamiento de una figura geométrica
En la figura 1 se muestra un polígono regular de 5 lados con los vértices [A, B, C, D, E] y se muestra la matriz correspondiente.

Figura 1. Polígono de 5 lados.
Representación matricial del polígono.

La figura 1 se encuentra en dos dimensiones representada en la matriz anterior, para el eje de las abscisas representado por R1 y el eje de las ordenadas corresponde a R2.
Traslación
Implica desplazar todos los puntos de una figura geométrica (circunferencias, triángulos, líneas, puntos), en la misma dirección y en la misma proporción. Supongamos la matriz anterior:

Para obtener una traslación de la figura en el eje de las abscisas y/u ordenadas se utiliza una matriz de traslación como la que se presenta a continuación:
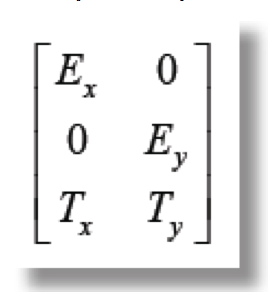
Donde TX representa traslación en x, Ty representa la traslación en y, de tal forma que si quisiéramos mover dos unidades en x a la figura y, una unidad en y quedaría expresada de la siguiente forma:

En la figura 2 se puede observar que el pentágono representa la figura original y la otra figura representa el pentágono trasladado.

Figura 2. Traslación del polígono.
Escalamiento
Es la operación que nos permite, dado un conjunto de puntos que representan una figura, aumentar o disminuir de tamaño el gráfico original. Regresamos nuevamente a la matriz de puntos que representa al pentágono.
Para obtener un escalamiento en x y/o en y se utiliza la siguiente matriz.

Anteriormente para la traslación utilizamos los parámetros Tx y Ty que representan traslación en X y traslación en Y respectivamente, ahora utilizaremos los parámetros Ex y Ey que servirán para escalar en X y en Y respectivamente. Si quisiéramos escalar a la figura en 2 veces el tamaño original, la operación de matrices quedaría de la siguiente forma:

A la operación anterior se le conoce como escalamiento compuesto, una combinación de traslación y escalamiento, quedaría representada por la figura 3.
Para representar un escalamiento simple asignamos a Tx y Ty un valor de 0, quedando representada por la figura 4.
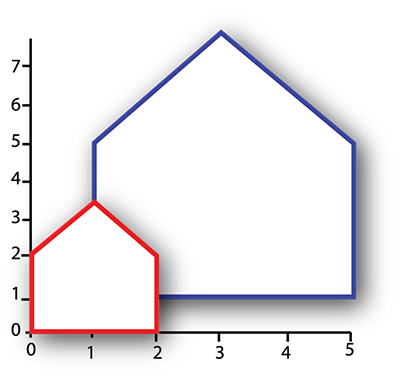
Figura 3. Escalamiento compuesto.

Figura 4. Escalamiento simple.
Rotación
Implica el cambio de orientación de una figura geométrica con respecto del punto de referencia. Veamos la siguiente propuesta para hallar la matriz de rotación (ver figura 5).
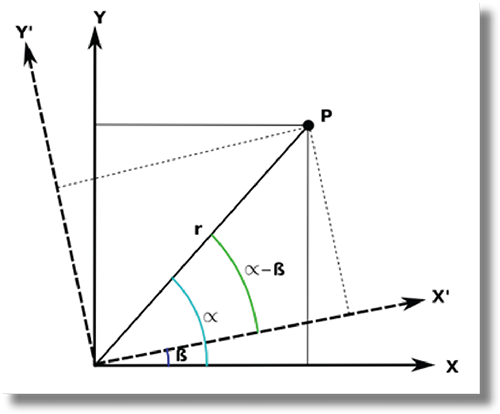
Figura 5. Deducción de rotación.
Note que la distancia r desde el origen al punto P es igual en ambos sistemas, de modo que las respectivas coordenadas (x, y) y (x’, y’) se pueden denotar de la siguiente forma:
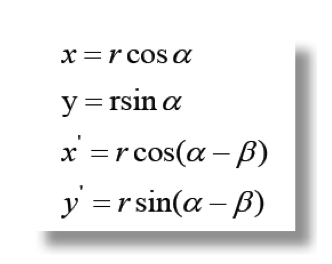
Tomando en cuenta identidades trigonométricas queda de la siguiente manera:

Tomando en cuenta la expresión AA y BB, la matriz de rotación quedaría así:

Esta matriz tiene como características poseer un determinante de 1 y ser ortogonal. En el siguiente ejemplo a través del pentágono anterior, propondremos rotarlo π radianes:

De tal manera que la figura rotada quedaría de la siguiente forma:

Figura 6. Rotación.
Un vistazo en 3D
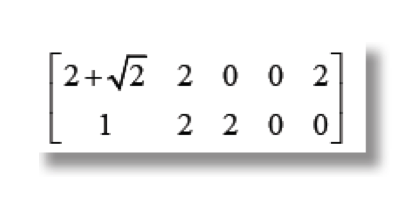
Hasta ahora hemos visto transformaciones en 2D (dos dimensiones), a continuación se explicarán las tres transformaciones anteriores (traslación, escalamiento y rotación) en 3D partiendo de una figura base. Cabe mencionar que el almacenamiento en matriz de una figura en 3D se hace en forma diferente en algunos programas de computadora donde se almacenan los planos de los que se compone una figura en 3D, a motivo de explicación nosotros seguiremos trabajando las figuras incluyendo sólo los vértices de la figura geométrica. Supongamos la siguiente matriz que representa a una figura en tercera dimensión.

Como notamos, la matriz anterior se incrementó en una dimensión, debido al soporte del eje z del gráfico en cuestión. Un apunte que debemos tomar en cuenta es que para el manejo de gráficos más complejos tendremos matrices de m x n dimensiones, donde se almacenarán no sólo las coordenadas de los gráficos sino el color, la textura, el estilo, entre otros.
Traslación y escalamiento en 3D
Para trasladar o escalar un gráfico en 3D recurriremos a la siguiente matriz:

Donde el parámetro E se utiliza como factor de escalamiento y el parámetro T como factor de traslación, como ya se vio anteriormente basta con sustituir estos parámetros con un número real para que se provoque una transformación en el gráfico.
Rotación en 3D
La rotación tridimensional se puede hacer de tres formas con respecto a cada uno de los ejes (x, y, z). Las matrices de rotación para cada uno de los ejes se presentan a continuación.
Respecto al eje z:

Respecto al eje y:

Respecto al eje x:

Las representaciones anteriores muestran claramente la matriz de rotación para cada uno de los ejes.
Vista computacional
Ahora veremos cómo usar este modelo de álgebra lineal aplicado a la programación, para lo cual utilizaremos el código del lenguaje de programación java para explicar cada uno de los casos en 2D.
1.-public class transformaciones{
2.-
3.-int matriz[][]=new int[5][3];
4.- public transformaciones(){
5.- matriz[][]={ 1, 3.41, 1,
6.- 2, 2, 1,
7.- 2, 0, 1,
8.- 0, 0, 1,
9.- 0, 2, 1
10.- };
11.-}
12.-public void trasladar(int incrementoX,
13.-int incrementoY) {
14.- for(int i = 0; i<5; i++){
15.-
16.-matriz[i][0]= matriz[i][0]+incrementoX;
17.-matriz[i][1]= matriz[i][0]+incrementoY;
18.-
19.- }
20.- }
21.-public void escalar(float escalarX, float
22.-escalarY){
23.-
24.-for(int i = 0; i<5; i++){
25.-
26.-matriz[i][0]= matriz[i][0]*escalarX;
27.-matriz[i][1]= matriz[i][0]*escalarY;
28.-
29.- }
30.- }
31.-public void rotar(float angulo){
32.-
33.-for(int i = 0; i< 5;i++){
34.-matriz[i][0]=
35.-matriz[i][0]*Math.cos(angulo) +
36.-matriz[i][1]*-1*Math.sin(angulo);
37.- int nuevaY =
38.-matriz[i][0]*Math.sin(rad)+
39.-matriz[i][1]*Math.cos(rad);
40.- tempY.set(i,nuevaY);
41.- }
42.-
43.- }
44.-}
45.-}
Explicación del código de programación
Definimos una nueva clase llamada transformaciones (línea 1), declaramos un nuevo arreglo que hará la función de una matriz (línea 3). Llenamos el arreglo con los vértices del polígono de 5 lados inicial con el constructor de la clase (líneas 4-11). Creamos un método llamado traslación el cual recibe por parámetros la traslación en el eje x y la traslación en el eje y, en seguida se utiliza una estructura de repetición para recorrer el arreglo, aplicar la traslación y construir la nueva matriz (líneas 12-20).
Creamos un método llamado escalamiento, el cual recibe por parámetros el escalamiento en el eje x y el del eje y, en la estructura de repetición multiplicamos cada uno de los espacios de memoria donde residen los vértices de la figura por el factor de escalamiento (líneas 21-30).
Creamos un método llamado rotación, el cual recibe por parámetro el ángulo en radianes dentro de la estructura de repetición, se aplican las operaciones correspondientes a cada uno de los renglones del arreglo para obtener una rotación de la figura (líneas 31-45).
CONCLUSIONES
En este trabajo se muestran cada una de las transformaciones lineales que son un tema del álgebra lineal, así como la relación con los gráficos por computadora.
Las transformaciones del álgebra lineal en la graficación por computadora han tomado un gran auge en la actualidad y es de gran importancia el estudio de modelos matemáticos que a través de una sinergia entre las ciencias computacionales provean de herramientas tales que puedan ser usadas en la computación moderna y a su vez por la sociedad en general.
El lector deberá probar y comprobar que el álgebra lineal describe en el ámbito de las transformaciones 2D y 3D, un modelo que se puede aplicar y entender fácilmente en los usos que hoy existen, como en los sistemas CAD, los juegos por computadora, entre otros.
Es de gran acierto enriquecer cada uno de los temas aquí presentados, entiendo así que el trabajo de este artículo es una guía que pretende introducir al lector para entender la influencia del álgebra lineal en la graficación por computadora.
BIBLIOGRAFÍA
Grossman, S. (1987). Applications for elementary Linear Algebra. E.U.A.: Iberoamericana.
Grossman, S. (2012). Álgebra lineal. E.U.A.: McGraw Hill.
Lay, D. (1999). Applications for elementary Linear Algebra. E.U.A.: Pearson Education.
Navas, E. (2010). Una humilde introducción a la graficación por computadora y otras yerbas. El Salvador: Centroamérica.